ESE
Embedded Software Engineering
Decoding Code 39
Code 3 of 9
Code 39 is a barcode with a full alphanumeric character set. Additionally,
it includes a unique start and stop code (*) and seven special characters
(- . $ / + % and space). The name 39 is derived from its code structure,
which consists of three wide elements out of a total of nine elements
- 3 of 9. These nine elements are comprised of five bars and four spaces.
An inter-character gap separates adjacent characters.
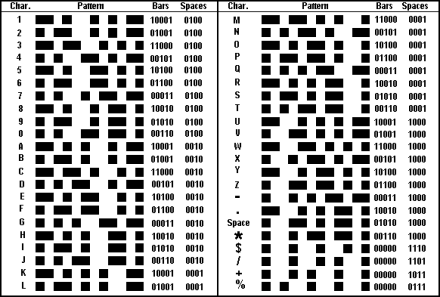
Table 1 - Code 39 Encoding
Code 39 uses just two element widths, characterized as narrow and wide.
By convention, a narrow element is called the X dimension. All X dimensions
must be of equal size within the symbol. The dimension of a wide element
is a multiple of X. This ratio can vary within certain limits but once
selected must remain consistent throughout the symbol. Generally, a wide
to narrow ratio in the range of 2:1 to 3:1 is acceptable.
Code 39 is classified as a discreet code, in that the characters each stand
alone being separated from each other by an inter-character gap. Since
the inter-character gap is not an integral part of the character encoding
it can be loosely toleranced, generally between X and 3X.
A special start/stop code is defined as an ASCII '*'. Its purpose is to
denote the leading and trailing ends of a Code 39 symbol. The bar/space
pattern of this code is unique and allows the symbol to be bi-directionally
scanned. Table 1 shows the Code 39 code assignments for all available characters.
Note how the last four characters in the table don't fit the established
coding pattern where all the other characters have two wide bars and one
wide space of the three wide elements. An example of the Code 39 character
"A" encoding is shown in Figure 1.
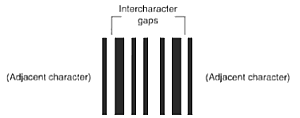
Figure 1 - Code 39 Character 'A' Encoding
Combining the discreet encoding attribute with the fixed 3 of 9 structure
results in a code that is classified as self checking. This makes the
possibility of a mis-decode much less likely since a substitution error
can only occur if two or more elements are misinterpreted. This could
happen, for example, if a spot on a narrow bar lined up with a void on
a wide bar in the same scan line and if the resulting bar pattern turned
out to be a legal Code 39 character.
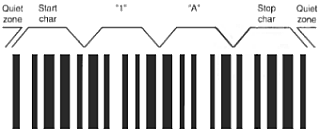
Figure 2 - A Complete Code 39 Barcode Symbol
In addition to the bars and spaces that make up a barcode characters
and the inter-character gaps that separate these characters, there is one
more component to a Code 39 symbol. This is the quiet zone, free and clear
of any printing, to either side of the "picket fence" pattern.
The quiet zone must be at least 10 times the X dimension. Now, with this
information we can take the pattern of bars and spaces to assemble a start
code, some data characters, and a stop code. Framing this with the requisite
quiet zones results in a complete barcode symbol shown in Figure 2.
Decoding 39
In keeping with my goal of providing a simplified development framework,
I'll demonstrate just the essence of a Code 39 decoding algorithm, which
is an implementation of the logic described in the AIM (Automatic Identification
Manufacturers) Reference Decode Algorithm for USS-39.
At this point it would be useful to make a couple of general observations.
The decode algorithm I'm presenting contains the basic steps for deciphering
a Code 39 symbol. The underlying logic is sound but ccould be expanded
upon. For example, you might wish to add secondary checks for acceleration,
inter-character gap, and absolute dimensions. Realize, that these secondary
checks could add as much code as the basic algorithm itself. As a result,
the underlying logic of the algorithm could be significantly obscured.
It's not unusual to encounter barcode labels that aren't up to the specification
for a variety of reasons. This may be due to dimensional tolerance problems, ink spread,
poor print contrast ratio, inadequate quiet zone, etc. And just because
the barcode label is deficient doesn't mean people don't expect you to be able
to read it. So these are good reasons why the reference decode algorithm
should be just a starting point.
- Confirm a leading quiet zone
- For each character:
- Measure the total character width and assign to S
- Compute the narrow/wide threshold as T = S/8
- Build a binary bit pattern representing the bars and spaces based on the threshold calculations
- Determine if the representative bit pattern matches a valid character
- The first character must be a start/stop code preceded by a quiet zone
- Continue processing until a valid start/stop code is found
- Confirm a trailing quiet zone
- Perform additional secondary checks as appropriate
You'll notice that the algorithm assumes the samples were collected in a forward
direction and makes no attempt to determine if the scan was actually performed in reverse.
To handle this situation, if the initial decode fails, the sample buffer is simply reversed
and the algorithm is invoked once again. This approach simplifies the code and its
testing.
A number of techniques can be applied to help the algorithm to read
marginal and out-of-spec barcode labels. Even with today's printer technology,
poor barcode labels continue to be produced. Generally, the problem lies
with the print contrast ratio and ink spread. Ink spread results in the
bars being larger and the spaces being proportionally smaller. As the decode
algorithm calculates the character width based on the total of all the
bars and spaces of the character, and the resulting narrow/wide threshold
is applied to both the bars and spaces, variations in the bars and spaces
for a given multiple of the X dimension can lead to decode problems. It
turns out that it's easy to employ an alternate technique to calculate
a separate threshold for the bars and a separate threshold for the spaces,
which is the way some of the newer Barcodes are designed. This techniques works well until you
get to the last four character in the Code 39 table. These don't conform to the established
code structure used by all the other characters where, of the three wide
elements, two are bars and one is a space; the last four characters all
have three wide spaces. A reasonable strategy would be to utilize the special
bar and space reference only if the primary algorithm fails to decode.
This is the tactic I take in my Code 39 decode algirithm.
The primary algorithm can also be enhanced by taking multiple iterations
through the sample buffer, judicially modifying the reference multiplier
on each pass. Although these tricks might be useful when trying to read
deficient symbols, you can be assured they're not going to improve your
mis-decode rate.
Optional Check Digit
A check digit is seldom used with Code 39 but if one is needed for a specific application there's a
standard method used to calculate one. The check digit is the modulo 43 sum of all the data character values in the
symbol. It is placed as the last data character of the symbol.
For Example
Data: 12345ABCDE/
Sum of data values: 1 + 2 + 3 + 4 + 5 + 10 + 11 + 12 + 13 + 14 + 40 = 115
115 divided by 43 = 2 with a remainder of 29
Referring to Table 2, 29 yields the character T, which is the check digit
Data with check digit: 12345ABCDE/T
Table 2 - Character/Value Set for Code 39 Check Character Calculation
Char Value Char Value Char Value Char Value
0 0 B 11 M 22 X 33
1 1 C 12 N 23 Y 34
2 2 D 13 O 24 Z 35
3 3 E 14 P 25 - 36
4 4 F 15 Q 26 . 37
5 5 G 16 R 27 space 38
6 6 H 17 S 28 $ 39
7 7 I 18 T 29 / 40
8 8 J 19 U 30 + 41
9 9 K 20 V 31 % 42
A 10 L 21 W 32