Decoding Interleaved Code 2 of 5

January 31, 2009 | John Dybowski

Interleaved Code 2 of 5
Interleaved Code 2 of 5 is a barcode with a numeric character set and unique start and stop patterns. The name derives from the way pairs of characters are encoded: two wide elements out of five. Code I2/5 uses the same encoding technique as Code 2/5 except it uses both the bars and spaces to represent data, thus providing higher data density. In the bar/space pattern, two digits are paired using the bars to represent the first digit and the spaces to represent the second. Each digit is made up of five bars or five spaces. For the characters (0 - 9) each character has two wide elements and three narrow elements.

Figure 1 - Code 2/5 and Code I2/5

Code I2/5 uses two element widths, described simply as narrow and wide. By convention, a narrow element is called the X dimension. All X dimensions must be of equal size within the symbol. The dimension of a wide element is a multiple of X. This ratio can vary within certain limits but once selected must remain consistent through the symbol. Generally, a wide to narrow ratio in the range of 2:1 to 3:1 is acceptable.

Code I2/5, unlike Code 2/5, is classified as a continuous barcode, as the symbol does not utilize an inter-character gap; all elements within the symbol contain information. Special start and stop patterns are defined to identify the leading and trailing ends of the barcode. The start code consists of four narrow elements starting with a bar. The stop code is made up of a wide bar followed by two narrow elements. The unique start/stop codes allow the symbol to be scanned bi-directionally.

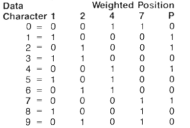
Table 1 - Code 2/5 Encoding

Table 1 shows the Code I2/5 character assignments for all available codes. Each symbol is made up of a series of one or more character pairs. Each pair is encoded using a series of five bars and five spaces. The bars encode the more significant digit of the pair and the spaces encode the less significant digit. The binary pattern for a digit derives from the weighted bit codes shown in table 1. From left to right, the bit positions are weighted 1, 2, 4, 7, and parity. Except for 0, the sum of the weighted bit positions directly yields the value of the encoded digit. The parity bit is used to give all characters even parity. Narrow elements are zero bits and wide elements are one bits. Figure 2 shows how character pars are encoded in the symbol. Figure 3 illustrates the start and stop pattern encoding. Figure 4 shows a complete Code I2/5 symbol.

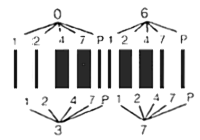
Figure 2 - Code I2/5 Digit Pair Encoding

The fixed 2 of 5 structure results in a code that is classified as self checking. This makes the possibility of a mis-decode much less likely since a substitution error can only occur if two or more elements are misinterpreted. This could happen if a spot on a narrow bar lined up with a void on a wide bar in the same scan line and if the resulting bar pattern turned out to be a legal code I2/5 character.

Because of the way the start and stop patterns are structured, a partial scan of an I 2/5 symbol may decode as a valid but shortened symbol. To prevent this, the symbol can include bearer bars that run along the top and bottom edges of the symbol in the scanning direction. This way, if a partial scan occurs, the scanning beam will hit the bearer bar and will not decode. The bearer bar must touch the top and bottom of all the bars and must be at least 3X wide. Another solution is to use a check digit. however, the most common solution is to set the decoding equipment to only accept symbols of a specific number of digits. So, although Code I2/5 allows encoding symbols of any length, in a specific application, the symbols must have a fixed length.

Figure 3 - Code I2/5 Start and Stop Codes

In addition to the bars and spaces that make up a barcode character, there is one more component to a Code I2/5 symbol. This is the quiet zone, which is free and clear of any printing, to either side of the bar/space pattern. The quiet zone must be at least 10 times the X dimension. Now, with this information we can take the bars and spaces to assemble a start pattern, some data characters, and a stop pattern. Framing this with the requisite quiet zones results in a complete barcode symbol as shown in figure 3.

Decoding I2/5

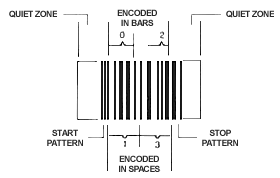
Figure 4 - Complete Code I2/5 Barcode Symbol

In keeping with my goal of providing a simplified development framework, I'll illustrate the essence of a I2/5 decode algorithm, which is an implementation of the logic described in the AIM (Automatic Identification Manufacturers) Reference Decode Algorithm for USS-I2/5.

The decode algorithm I'm presenting contains the basic steps for deciphering a code I2/5 symbol. The underlying logic is sound but could be enhanced. For example, you might want to add secondary checks for acceleration, inter-character gap, and absolute dimensions. These secondary checks and balances could add as much code as the basic algorithm itself, significantly obscuring the underlying logic.

It's not unusual to encounter barcode labels that don't meet specification. This may be due to dimensional tolerance problems, ink spread, poor print contrast ratio, inadequate quiet zone, etc. And just because the barcode is deficient doesn't mean people don't expect you to be able to read it. So these are good reasons why a good decode algorithm should be just a starting point. The essential steps of the code I2/5 decode algorithm are:
The decode algorithm assumes the samples were collected in a forward direction and doesn't perform any special processing to determine if the scan was actually performed in reverse. In order to handle this, if the initial decode fails, the sample buffer is simply reversed and the algorithm is invoked again. This approach makes the code simpler and easier to test.

A common print defect, still often encountered, is a phenomenon called ink spread, which makes the bars larger and the spaces proportionally smaller. An effective way to deal with this is to process the bars separately from the spaces. In my decode algorithm I use both the traditional reference calculation described above along with an alternate reference calculation that computes separate reference thresholds for the bars and spaces. The tactic is to attempt to decode the symbol using the traditional reference calculation first. If that fails, the separate bar/space reference is tried.

Optional Checksum
A check digit is not required for Code 25 but data security can be increased through the use of one. The standard way to calculate a Code 25 check digit is as a modulo 10 based on alternating 1, 3 weightings of the data characters. The weighting is arranged so the least significant digit, the digit on the far right of the symbol, receives the 3 weight.

As an example, the check digit would be calculated as follows for the following data characters:

      Data Characters  4 3 8 2 7
      Weighting        3 1 3 1 3
Weighted Sum = (3X4) + (1X3) + (3X8) + (1X2) + (3X7) = 42

The check digit is the digit which when added to the weighted sum produces a sum ending in 0. Thus, the check digit for the example is 8. The check digit is placed as the last data character of the symbol, the least significant digit.

Data with check digit = 4 3 8 2 7 8