Decoding Codabar

January 31, 2009 | John Dybowski

Codabar
Codabar (sometimes called Code 2 of 7) is a discrete, self-checking, width-modulated barcode with a character set providing the digits (0 - 9) and the special characters (- $ : / . +). Additionally, there are four unique start/stop codes represented by the characters A, B, C, and D.

Unlike the other width-modulated barcodes, Codabar doesn't use narrow and wide element widths to directly encode the ones and zeros of the character set. Instead, it specifies a total of 18 different sets of bar and space widths. A fundamental characteristic of the Codabar encoding is that the bars are decoded independently of the spaces. This structure was designed to accommodate the printing errors characteristic of some early printers.

Each Codabar character is represented by seven elements: four bars and three spaces. Of the seven elements, either two or three will be wide, and the rest will be narrow. The lack of a fixed number of wide elements per character lowers the data integrity of Codabar relative to other barcodes. An inter-character gap, that is not part of the character itself, separates the characters within the symbol. For the numeric characters (0-9) and two of the special characters ($ -), there are two wide elements out of the seven elements. These are encoded using one wide bar and one wide space. The remaining special characters (:, /, ., +) and the start/stop characters (A B C D) use three wide elements. The special symbols are encoded using three wide bars. The start/stop codes are encoded using one wide bar and two wide spaces. Note that the encoding provides a constant character length regardless of whether two or three elements of the character are wide. The Codabar character set encoding is shown in table 1.

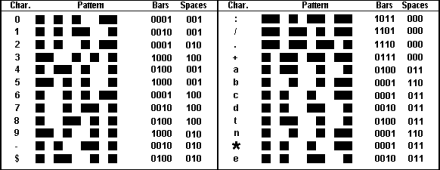
Table 1 - Codabar Encoding

By convention, a narrow element is called the X dimension and all X dimensions must be of equal size within the symbol. The dimension of a wide element is a multiple of X. This ratio can vary within certain limits but once selected remains consistent over the symbol. Generally, a wide to narrow ratio in the range of 2:1 to 3:1 is acceptable.

Codabar is classified as a discreet code, in that the characters each stand alone being separated from each other by an inter-character gap. Since the inter-character gap is not an integral part of the character encoding its dimension isn't critical and is generally made between X and 3X.

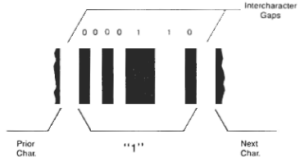
Figure 1 - Codabar Character '1' Encoding

Unlike other barcode symbologies, Codabar has four different start/stop codes, represented by the characters (A B C D). Any one of these can be used as a start code or stop code. The start/stop codes are generally used in matching pairs and and can only be used on each end of the symbol. The lack of a single start and stop code lowers the data integrity of Codabar compared to other Barcodes. In addition to framing the symbol, the choice of the start/stop codes can convey information, thus, most barcode readers provide the option of whether or not to transmit the start and stop codes as part of the symbol. An example of the codabar character "1" encoding is shown in Figure 1.

Figure 2 - Complete Codabar Barcode Label

In addition to the bars and spaces that make up a barcode character and the inter-character gaps that separate these characters, there is one more component to a barcode label. This is the quiet zone, free of any printing, to either side of the bar/space pattern. The quiet zone should be a minimum of 10X. Now, with this information we can take the pattern of bars and spaces to assemble a start code, some data characters, and a stop code. Framing this with the requisite quiet zones results in a complete barcode symbol shown in figure 2.

Decoding Codabar
The essence of a codabar decoding algorithm is an implementation of the logic described in the AIM (Automatic Identification Manufacturers) Reference Decode Algorithm for USS-Codabar.

Keep in mind that this is a basic algorithm. The underlying logic is sound but can be significantly expanded. You might want to add secondary checks for acceleration, inter-character gap, and absolute dimensions. Realize, that these secondary checks could add as much code as the basic algorithm itself. As a result, the underlying logic of the algorithm would be obscured.

It's not unusual to encounter barcode labels that aren't up to the specification for a variety of reasons. This may be due to dimensional tolerance problems, ink spread, poor print contrast ratio, inadequate quiet zone, etc. Just because a barcode is deficient doesn't mean people don't expect you to be able to read it. These are good reasons why a working decode algorithm is just a starting point.

The basic steps of the codabar decode algorithm are:

Note that the algorithm allways assumes the samples were collected in a forward direction and doesn't, in itself, handle a reverse scan. Instead, this is handled by the calling function. If the initial decode fails, the sample buffer is reversed and the algorithm is once again invoked. This approach tends to simplify the coding and associated test requirements.

Optional Checksum
A check digit is seldom used in Codabar and there's no de facto standard for one. However, for applications that require enhanced data security, a check character may be used using an appropriate calculation scheme.

When a check character is used, it's positioned after the last data character, immediately before the stop character. The check character is calculated as follow:

  1. Each Codabar character is assigned a numerical value as shown in Table 2.
  2. Take the sum of all the numerical values of all characters, including start and stop, modulo 16.
  3. The character whose value is the difference between the sum and 16 is used as the check character.
  4. This way the modulo 16 sum of the full symbol with check character becomes 0.
For example, the check digit would be calculated as follows for a symbol consisting of the data characters "A37859B"

      Data Characters  A  3  7  8  5  9  B
      Assigned value   16 3  7  8  5  9  17
The resulting sum is: 65 mod 16 = 1

The difference (16 - 1) = 15. Consulting the conversion table yields a check character of "+". The check digit is placed as the last data character of the symbol, preceding the stop character.

Data with check digit = "A37859+B

Table 2 - Numerical Codabar Character Assignments for Check Digit Calculation
Char Value Char Value Char Value Char Value 0 0 5 5 - 10 + 15 1 1 6 6 $ 11 A 16 2 2 7 7 : 12 B 17 3 3 8 8 / 13 C 18 4 4 9 9 . 14 D 19