ESE
Embedded Software Engineering
Barcode
Kartrak
Kartrak
After overcoming numerous technical obstacles, the read rate was purportedly comparable with many of today's UPC readers. This ultimately led to the installation of about 1000 readers and the bar coding of approximately 1.8 million railroad cars. In addition, 200,000 "piggyback" tractor trailer containers were also barcoded. The readers were usually situated at junctions, interchanges, and entrances to rail yards. Kartrak usage peaked in 1968 and then saw a gradual decline due primarily to inadequate label maintenance. Today only about 50 scanners are still in operation.
Encoding Techniques
Barcodes are composed of a series of dark bars and light bars (or bars and spaces) that, when properly combined, represent letters, numbers, and other symbols. The bars and spaces are organized according to specific rules based on the particular barcode symbology. Barcodes work with the fundamentals of digital logic - ones and zeros - and are binary in form. That's not to say that human-readable characters are not placed on barcode labels, but they are provided for information purposes only and are not electrically deciphered; computer information and human information are kept separate.
Many different barcode symbologies exist, each being optimized for a specific application. Trade offs are made between conflicting properties retaining those that are necessary for a given purpose. I'll look at several of the simpler, more popular barcode structures more closely, but first let me touch on some fundamental concepts.
The smallest element from which a barcode is formed is called a module, also sometimes referred to as the "X" dimension. The wider bars and spaces are, in most cases, integer multiples of a module. These relationships remain consistent as the codes are magnified or reduced in overall size and as they are scanned at different velocities.
Modules, as applied to bars and spaces, work to translate the optical barcode into a digital code. Most barcodes are binary in nature and are composed of ones and zeros. The way these ones and zeros are extrapolated from the bar/space pattern varies depending on the specific barcode. In some cases wide elements are interpreted as ones and narrow elements as zeros. Other barcodes assign binary values to dark and light elements. In such a scheme a dark bar that spans several module dimensions accumulates the respective number of one bits. Zeros are accumulated similarly using spaces of varying width.
There are different ways these fundamental bit encoding techniques are applied to creating a barcode's character set. Some Barcodes use only the bars to represent data bits with the spaces used merely as separators. Others use both bars and spaces to form a single code representation of a character. Another method using both bars and spaces interleaves the coded characters where the bars encode the odd characters and the even characters are encoded in the spaces. A variety of other techniques are also used but these are the most common.
One assumption on which barcode decoding algorithms rest is that the absolute velocity at which the barcode is scanned and the absolute size of the bar/space elements are unimportant. Provided the scanning velocity (and variation in velocity) does not deviate beyond a given limit, the relative module relationship between bars and spaces can be determined by a comparison of the bar and space widths in the time domain. The four most common bit-level encoding techniques are shown in the figure below. Note that UPC defines both left- and right-handed symbols for the same character. Using these as an example lets look at some basic bit recovery techniques.
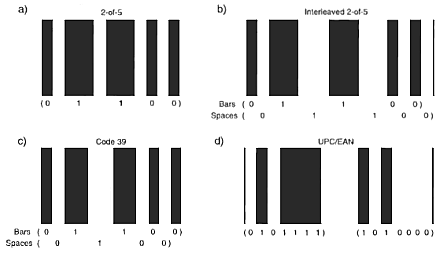
Four different Barcode encoding techniques
Code 39 and Codabar are representative of types that can be most easily understood as composed of dark bars and light bars rather than bars and spaces since both the bars and spaces take part in encoding a character. The interpretation of wide and narrow elements in these barcodes is the same as in the other codes I just described.
Finally, some codes, such as UPC, are structured such that bars denote one bits and spaces denote zero bits. With UPC, width measurements are usually accomplished by making comparisons between a bar and its associated space and the next bar and its associated space.
There are a certain characteristics that are important to be aware of when evaluating different barcode symbologies. Let me introduce these concepts here and I'll elaborate more fully as I look at specific barcode symbologies in more depth a little later.
First, some codes are classified as continuous and others as discreet. These terms describe the way encoded characters are concatenated to form a multi-character symbol. In a continuous code the inter-character space is part of the code structure and must adhere to strict dimensional tolerances as defined in the code specification. In a discreet code the intercharacter space is just a separator and not part of the code; its width can vary within fairly wide dimensional limits.
Second, some codes are designed in such a manner that they are self checking. This refers to the fact that an algorithm can be applied to each character so a mis-decode requires two independent printing defects within the same character in the same scan line.
Finally, for added data security a check digit can be included in the barcode. With some codes this is mandatory whereas others allow the check digit as an option. In either case the Barcode specification generally specifies how the check digit should be calculated for a given Barcode. Generally, the check digit is treated as an inherent part of the Barcode as far as the decoding equipment goes. That is, if the check calculation does not yield the expected result, the reader treats the operation as a no-decode.
Two of Five
One of the simplest and most straightforward barcodes is code 2/5. Having its origin in the late 1960s, this numeric-only code has seen use in sequentially numbering airline tickets, photo finishing, and warehouse sorting.

Code 2 of 5
Data is encoded using a modified binary method where the bar positions from left to right are assigned weighting factors of 1, 2, 4, 7, and parity. The zero character is the exception to this rule. In addition to the numeric symbols a distinctive start code and stop code are defined allowing bidirectional scanning. The character set encoding for code 2/5 defines the numbers 0-9 and the unique start and stop codes.
The code 2/5 structure is also categorized as self checking since all characters are composed of two wide bars and three narrow bars. This is where the name comes from since two of the five bars must always be wide.
Interleaved Two of Five
Developed in 1972, code I2/5 attains a higher character density than 2/5 by utilizing the spaces as well as the bars for encoding data characters. The actual encoding methodology is identical to that used in code 2/5. This code has seen use in warehousing and heavy industrial applications as well as in the automotive industry.

Interleaved code 2 of 5
Note that by placing information in the spaces as well as the bars code I2/5 is no longer a discreet code like code 2/5. It does, however, retain its self checking attribute.
Three of Nine
This full alpha-numeric code 39 was developed in 1975. It's the standard barcode used by the United States Department of Defense, and is also used by the Health Industry Bar Code Council.

Code 3 of 9
Codabar
in 1972 and has been used by U.S. blood banks, photo labs, and on FedEx air bills. Codabar provides 16 characters including the digits 0 through 9 and the characters '-', '$', ':', '.', and '+'. It also includes 4 unique start/stop codes designated 'A', 'B', 'C', and 'D'. All Codabar characters are formed of seven elements made up of 4 bars and 3 spaces. Each bar or space can be narrow or wide. Wide elements are interpreted as a 1 bits and narrows as a 0 bits. Bit recovery utilizes bar-to-bar and space-to-space comparisons that results in a binary number that is checked against a table of valid characters. Codabar is a discreet, self checking code.

Codabar
Multi-Dimensional Codes
The codes I've described thus far use only one dimension for information storage. There is a limit to how much data can practically be encoded using this, essentially serial, method. Using two dimensions for data storage results in a substantially higher volume of data per unit size. However, this does rule out the use of an inexpensive, hand motivated scanner. Moving beam laser scanners, CCD scan heads, and cameras prove suitable for this purpose. These devices are available in fixed base or hand held configurations.
The capability of packing more information into a given area can be useful in a number of ways. The most obvious is to simply store more information. Less obvious is to provide enhanced data integrity using the extra storage to provide data redundancy and, more importantly, error detection/correction information. If the error recovery mechanism is implemented properly, a label can be accurately read even if substantial portions have been damaged or obscured by dirt.

CodaBlock - 65 characters and Code 49 - 26 characters
The simpler 2-D codes start with existing symbologies and add the required control information to handle longer records and to ensure data accuracy. CodaBlock, which is based on code 39 with additional control information and check digits uses this approach.

VeriCode - 185 characters and Data Matrix - 68 characters
Another strategy is to combine computer science disciplines with a formal data redundancy/error correction regimen that detaches the symbology from its traditional barcode precursors. Only the optical scanning characteristics are retained. Representative of this class are VeriCode and Data Matrix.